SO3_SE3_spatialmath¶
# !pip install spatialmath-python
spatialmath¶
from spatialmath import SO3
A rotation of 0.3 radians about the x-axis:
R1 = SO3.Rx(0.3)
R1
1 0 0
0 0.9553 -0.2955
0 0.2955 0.9553
A rotation of 30 deg about the z-axis:
R2 = SO3.Rz(30, 'deg')
R2
0.866 -0.5 0
0.5 0.866 0
0 0 1
R2.angvec()
(0.5235987755982988, array([0., 0., 1.]))
李群李代数¶
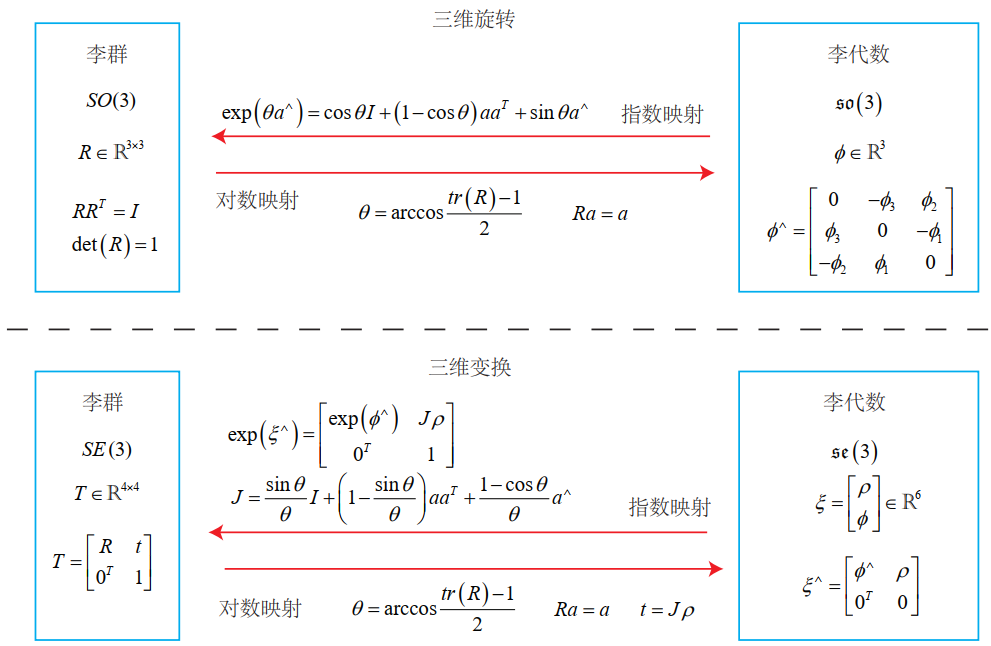
特殊正交群 \(SO(3)\)¶
三维旋转矩阵\(\boldsymbol{R}\)构成了特殊正交群\(SO(3)\):
\[
SO(3)=\left\{\boldsymbol{R} \in \mathbb{R}^{3 \times 3} \mid \boldsymbol{R} \boldsymbol{R}^{T}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\}
\]
三维旋转向量\(\phi\)是一种李代数\(so(3)\):
\[
so(3) = \left\{\phi \in \mathbb{R}^{3}, \Phi = \boldsymbol{\phi}^{\wedge} \in \mathbb{R}^{3 \times 3}\right\}
\]
其对应的反对称矩阵如下:
\[\begin{split}
\boldsymbol{\phi}^{\wedge} = \boldsymbol{A} =
\left[\begin{array}{ccc}
0 & -\phi_{3} & \phi_{2} \\
\phi_{3} & 0 & -\phi_{1} \\
-\phi_{2} & \phi_{1} & 0
\end{array}\right],\quad \boldsymbol{A}^{\vee} = \phi
\end{split}\]
两者转换公式如下:
\[
\boldsymbol{R}=\exp \left(\boldsymbol{\phi}^{\wedge}\right)
\]
\[
\boldsymbol{R}^{-1}=\exp \left((-\boldsymbol{\phi})^{\wedge}\right)
\]
\[
\phi = \ln \left(\exp \left(\boldsymbol{\phi}^{\wedge}\right)\right)^{\vee} = \ln(\boldsymbol{R})^{\vee}
\]
我们使用了\(^\wedge\)和\(^\vee\)符号来指代“从向量到矩阵”和“从矩阵到向量”的关系。
三维向量的反对称矩阵:
from spatialmath.base import skew, vex
skew([1, 2, 3])
array([[ 0, -3, 2],
[ 3, 0, -1],
[-2, 1, 0]])
验证 \(\boldsymbol{R}=\exp \left(\phi^{\wedge}\right)\):
from spatialmath.base import trexp
R1 = SO3.Rx(0.3)
trexp([1, 0, 0], 0.3), R1.A
(array([[ 1. , 0. , 0. ],
[ 0. , 0.95533649, -0.29552021],
[ 0. , 0.29552021, 0.95533649]]),
array([[ 1. , 0. , 0. ],
[ 0. , 0.95533649, -0.29552021],
[ 0. , 0.29552021, 0.95533649]]))
验证 \(\boldsymbol{\phi} = \ln(\boldsymbol{R})^{\vee}\):
vex(R1.log()), R1.angvec()
(array([0.3, 0. , 0. ]), (0.3, array([1., 0., 0.])))
特殊欧氏群 \(SE(3)\)¶
同样变换矩阵\(\boldsymbol{T}\)构成了特殊欧氏群\(SE(3)\):
\[\begin{split}
S E(3)=\left\{\boldsymbol{T}=\left[\begin{array}{cc}
\boldsymbol{R} & \boldsymbol{t} \\
\mathbf{0}^{T} & 1
\end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{R} \in S O(3), \boldsymbol{t} \in \mathbb{R}^{3}\right\}
\end{split}\]
李代数\(se(3)\)记作\(\boldsymbol{\xi}\),是一个六维向量。前三维为平移,记作\(\rho\):
\[\begin{split}
se(3) = \left\{\boldsymbol{\xi}=\left[\begin{array}{c}
\rho \\
\phi
\end{array}\right] \in \mathbb{R}^{6}, \boldsymbol{\rho} \in \mathbb{R}^{3}, \boldsymbol{\phi} \in \mathfrak{s o}(3), \boldsymbol{\xi}^{\wedge}=\left[\begin{array}{ll}
\boldsymbol{\phi}^{\wedge} & \boldsymbol{\rho} \\
\mathbf{0}^{T} & 0
\end{array}\right] \in \mathbb{R}^{4 \times 4}\right\}
\end{split}\]
对应的反对称矩阵:
\[\begin{split}
\boldsymbol{\xi}^{\wedge}=\left[\begin{array}{ll}
\boldsymbol{\phi}^{\wedge} & \boldsymbol{\rho} \\
\mathbf{0}^{T} & 0
\end{array}\right] \in \mathbb{R}^{4 \times 4}
\end{split}\]
两者转换公式如下: $\(T = \exp \left(\boldsymbol{\xi}^{\wedge}\right)\)$
\[T^{-1} = \exp \left((-\boldsymbol{\xi})^{\wedge}\right)\]
\[\boldsymbol{\xi} = \ln \left(\exp \left(\boldsymbol{\xi}^{\wedge}\right)\right)^{\vee}=\ln (T)^{\vee}\]
from spatialmath import SE3
T = SE3.Ry(0.3)
T
0.9553 0 0.2955 0
0 1 0 0
-0.2955 0 0.9553 0
0 0 0 1
验证\(\boldsymbol{\xi} = \ln (T)^{\vee}\),如下:
from spatialmath.base import vexa
vexa(T.log())
array([0. , 0. , 0. , 0. , 0.3, 0. ])
验证\(\boldsymbol{\xi}^{\wedge} = \ln(T)\),如下:
from spatialmath.base import skewa
print(skewa([0. , 0. , 0. , 0. , 0.3, 0.]), '\n')
print(T.log())
[[ 0. -0. 0.3 0. ]
[ 0. 0. -0. 0. ]
[-0.3 0. 0. 0. ]
[ 0. 0. 0. 0. ]]
[[ 0. 0. 0.3 0. ]
[ 0. 0. 0. 0. ]
[-0.3 0. 0. 0. ]
[ 0. 0. 0. 0. ]]
验证\(T = \exp \left(\boldsymbol{\xi}^{\wedge}\right) = \exp(\ln(T))\),如下:
print(T.A, '\n')
print(trexp(T.log()))
[[ 0.95533649 0. 0.29552021 0. ]
[ 0. 1. 0. 0. ]
[-0.29552021 0. 0.95533649 0. ]
[ 0. 0. 0. 1. ]]
[[ 0.95533649 0. 0.29552021 0. ]
[ 0. 1. 0. 0. ]
[-0.29552021 0. 0.95533649 0. ]
[ 0. 0. 0. 1. ]]
旋转表示¶
第\(i\)帧和第\(j\)帧之间的相对位姿,在李群\(SE(3)\)上可以表示为:
\[
\boldsymbol{T}_{i,j} = \boldsymbol{T}_i^{-1}T_j
\]
也可以在李代数上表示为:
\[\begin{split}
\begin{aligned}
\boldsymbol{\xi}_{i j} &=\ln \left(\boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j}\right)^{\vee} \\
&=\ln \left(\exp \left(\left(-\boldsymbol{\xi}_{i}\right)^{\wedge}\right) \exp \left(\boldsymbol{\xi}_{j}^{\wedge}\right)\right)^{\vee}
\end{aligned}
\end{split}\]
