Lidar with Rotation¶
import numpy as np
from scipy.spatial.transform import Rotation as sciR
基本知识¶
线速度¶
\(\omega\)为角速度（三维向量），\(r\)为旋转半径（三维向量），那么线速度为：
\[
\dot{r} = \omega \times r
\]
E.g.，假设IMU围绕x轴旋转，如果某点位于x轴上，此时该点旋转半径r和x轴重合，其线速度为0：
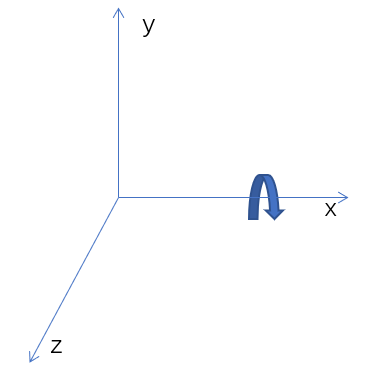
r = [1, 0, 0]
w = [2, 0, 0] # 逆时针为正，右手法则
np.cross(w, r)
array([0, 0, 0])
若某物体在该点\((1, 0, 0)\)的姿态和IMU姿态一致（即\(R\)为单位阵），其角速度应该等于IMU角速度：
\[
\omega' = R \omega
\]
R = np.eye(3, 3)
R @ w
array([2., 0., 0.])
E.g.，假设IMU围绕y轴逆时针旋转，如果某点位于x轴上，其线速度方向应该为z轴的负方向：
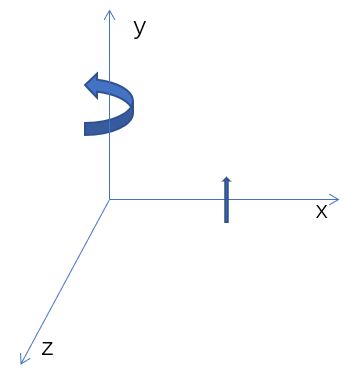
r = [1, 0, 0]
w = [0, 2, 0]
np.cross(w, r)
array([ 0, 0, -2])
角速度和自身坐标系关系¶
角速度的积分得到的旋转向量\(\phi=\boldsymbol{\omega}_{k-1}\left(t_{k}-t_{k-1}\right)\)为\(t_k\)变换到\(t_{k-1}\)下的变换，而不需要求逆！因为此时是坐标系变换，等于参考向量被反向旋转。
例如IMU（坐标系）围绕自身x轴转90度（新x轴不变，新y轴为原来z轴，新z轴为原来-y轴），那么原来坐标系中的向量\([0, 1, 0]\)在新的坐标系下表示为\([0, 0, -1]\)，对\([0, 0, -1]\)做变换看是否等于原向量\([0, 1, 0]\)：
from scipy.spatial.transform import Rotation as sciR
R = sciR.from_rotvec(np.pi/2 * np.array([1, 0, 0]))
R.apply([0, 0, -1]).round()
array([ 0., 1., -0.])
汽车拐弯模拟¶
假设汽车以\(10 \text{m/s}\)速度和\(30^\circ \text{/s}\)角速度拐弯：
import matplotlib.pyplot as plt
w = np.array([0., 0., np.deg2rad(30)]) # 角速度
v = np.array([0., 10.0, 0.]) # 线速度 m/s
p = np.array([0., 0., 0.]) # 位置
dt = 0.01 # second
p_hst = [] # history of position
for i in range(300):
R = sciR.from_rotvec(i*w*dt)
p = p + R.inv().apply(v) * dt
p_hst.append(p)
p_hst = np.array(p_hst)
plt.plot(p_hst[:, 0], p_hst[:, 1])
plt.xlim(0, 30)
plt.ylim(0, 30)
plt.show()
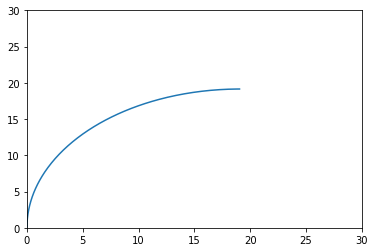
上面求当前旋转矩阵时是先求出相对\(t_0\)时刻转过的角度（\(w_1 \cdot \Delta t_1 + w_2 \cdot \Delta t_2 +\ ......\)），代码里假设了角速度和时间间隔不变：
R = sciR.from_rotvec(i*w*dt)
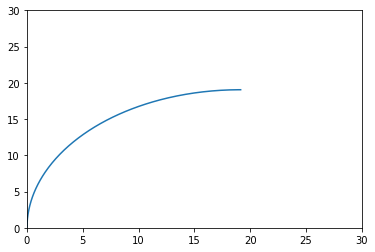
实际使用时应该采用积分形式，例如下面是旋转矩阵积分：
\[
R_t = R_{t-1} e^{\phi_\times}
\]
对应代码R = R * sciR.from_rotvec(w*dt)。
import matplotlib.pyplot as plt
w = np.array([0., 0., np.deg2rad(30)]) # 角速度
v = np.array([0., 10.0, 0.]) # 线速度 m/s
p = np.array([0., 0., 0.]) # 位置
dt = 0.01 # second
R = sciR.from_rotvec([0., 0., 0.])
p_hst = [] # history of position
for i in range(300):
R = R * sciR.from_rotvec(w*dt)
p = p + R.inv().apply(v) * dt
p_hst.append(p)
p_hst = np.array(p_hst)
plt.plot(p_hst[:, 0], p_hst[:, 1])
plt.xlim(0, 30)
plt.ylim(0, 30)
plt.show()
4D雷达¶
雷达转动和位移的影响¶
Aqronos雷达扫描方式是4微秒一个点，所以点云是在时序上扫描得到的，对应一组连续的雷达坐标系。
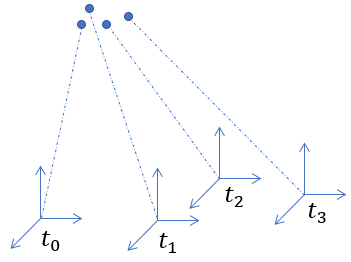
计算一个刚体的运动速度需要利用该刚体上多点的位置和速度信息，因此需要把所有的点转换到同一个坐标系中表示，这样各点的相对位置才准确。
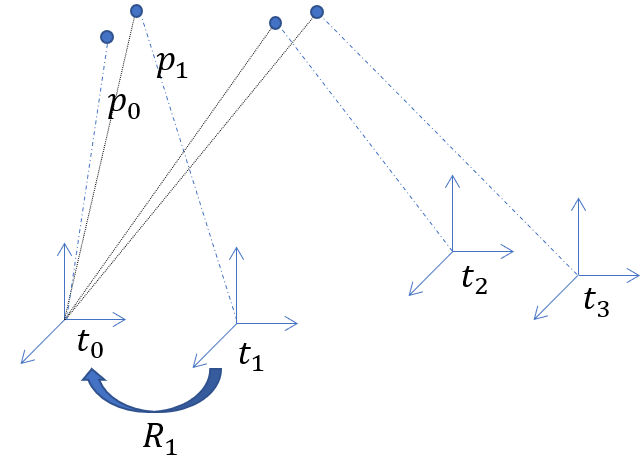
设三维空间中一个目标点在\(t_1\)时刻雷达坐标系下为\(\vec{p}_1\)，将该点转换到\(t_0\)时刻雷达坐标系下为：
\[
\vec{p}_0 = R_1\vec{p}_1 + \vec{l}
\]
其中\(R_1\)为雷达坐标系\(t_1\)时刻相对\(t_0\)时刻的姿态，\(l\)为雷达位移。两边同时对求导可得：
\[\vec{v}_0 = \dot{R}_1\vec{p}_1 + R_1\vec{v}_1 + \vec{v}_l\]
其中\(\dot{R} = R \omega_{\times},\ (\omega \times \vec{a} = \omega_{\times}a)\)。
由于雷达测量点的速度\(v'_1\)为该点相对雷达的速度在雷达发射方向上的投影\(v'_1 = \vec{p}_1 \cdot \vec{v}_1\)，带入上面公式可得：
\[\vec{p}_1 R_1^T \vec{v}_0 = (\omega \times \vec{p}_1) \cdot \vec{p}_1 + v'_1 + (R_1^T\vec{v}_l) \cdot \vec{p}_1\]
由于\((\omega \times \vec{p}_1) \cdot \vec{p}_1 = 0\)，而\((R_1^T\vec{v}_l) \cdot \vec{p}_1\)相当于汽车速度在雷达发射方向上的投影，移项得到：
\[
(\vec{p}_1 R_1^T) \cdot (\vec{v}_0 - \vec{v}_l) = v'_1
\]
同理可得其他点，并组成\(Ax = B\)的形式（这里假设雷达速度\(\vec{v}_l\)不发生变化）：
\[\begin{split}
\begin{bmatrix}
\vec{p}_1 R_1^T \\
\vec{p}_2 R_2^T \\
\vdots \\
\vec{p}_n R_n^T
\end{bmatrix} (\vec{v}_0 - \vec{v}_l) =
\begin{bmatrix}
v'_1\\
v'_2\\
\vdots \\
v'_n
\end{bmatrix}
\end{split}\]
def generatePoints(xc, yc, zc, n, xs=1, ys=1, zs=1):
"""
@xc, yc, zc: points center
@xs, ys, zs: points scale
"""
points = np.random.rand(3, n)
points[0] = points[0]*xs + xc
points[1] = points[1]*ys + yc
points[2] = points[2]*zs + zc
return points
generatePoints(10, 50, 1, n=2)
array([[10.31871359, 10.2151918 ],
[50.2594425 , 50.140402 ],
[ 1.8613003 , 1.40457554]])
Simulator：
from scipy.spatial.transform import Rotation as sciR
class Simulator:
def __init__(self, w, v, vt, p, dt):
self.w = w # 角速度
self.v = v # 雷达速度
self.vt = vt # 目标速度
self.p = p # 雷达起始位置
self.dt = dt # 间隔时间
self.R = sciR.from_rotvec([0., 0., 0.]) # 单位阵
@staticmethod
def generateTargetPoints(xc, yc, zc, n, xs=1, ys=1, zs=1):
"""
@xc, yc, zc: points center
@xs, ys, zs: points scale
"""
points = np.random.rand(3, n)
points[0] = points[0]*xs + xc
points[1] = points[1]*ys + yc
points[2] = points[2]*zs + zc
return points # shape: 3 x n
def run(self):
w = self.w # 角速度
v = self.v # 雷达速度 m/s
vt = self.vt # 目标速度 v-target
p = self.p # 雷达起始位置
dt = self.dt # second
tps = self.tps # target points
R = sciR.from_rotvec([0., 0., 0.])
A = []
B = []
for i in range(len(self.tps)):
R = R * sciR.from_rotvec(w*dt)
p = p + R.inv().apply(v) * dt
tp = tps[:, i] + vt*dt # target point
p_t = tp - p
A.append(R.apply(p_t))
B.append(R.inv().apply(vt-v)@p_t)
return A, B
w = np.array([0., 0., np.deg2rad(30)]) # 角速度
v = np.array([0., 10.0, 0.]) # 雷达速度 m/s
vt = np.array([2., 0., 5.]) # 目标速度 v-target
p = np.array([0., 0., 0.]) # 雷达起始位置
dt = 0.01 # second
Sim = Simulator(w, v, vt, p, dt)
Sim.tps = Simulator.generateTargetPoints(10, 50, 1, n=10) # target points
A, B = Sim.run()
print("gt:", vt)
print("estimation:", (np.linalg.pinv(A)@B + v).round(2))
gt: [2. 0. 5.]
estimation: [2. 0. 5.]
如果不考虑旋转，看下求解的目标速度和真值（gt）的误差情况：
# !pip install jdc
import jdc
%%add_to Simulator
def run_no_rotation(self):
w = self.w # 角速度
v = self.v # 雷达速度 m/s
vt = self.vt # 目标速度 v-target
p = self.p # 雷达起始位置
dt = self.dt # second
tps = self.tps # target points
R = sciR.from_rotvec([0., 0., 0.])
A = []
B = []
for i in range(len(self.tps)):
R = R * sciR.from_rotvec(w*dt)
p = p + R.inv().apply(v) * dt
tp = tps[:, i] + vt*dt # target point
p_t = tp - p
A.append(p_t)
B.append(R.inv().apply(vt-v)@p_t)
return A, B
A, B = Sim.run_no_rotation()
print("gt:", vt)
print("estimation:", (np.linalg.pinv(A)@B + v).round(2))
gt: [2. 0. 5.]
estimation: [11.57 -2.18 11.27]
Sim.w = np.array([0., 0., np.deg2rad(30)]) # 角速度
Sim.v = np.array([0., 10.0, 0.]) # 雷达速度 m/s
Sim.vt = np.array([20., 30., 5.]) # 目标速度 v-target
Sim.dt = 0.00004 # 40us
A, B = Sim.run_no_rotation()
print("gt:", Sim.vt)
print("estimation:", (np.linalg.pinv(A)@B + Sim.v).round(3))
gt: [20. 30. 5.]
estimation: [20.133 29.97 5.084]
Sim.w = np.array([0., 0., np.deg2rad(30)]) # 角速度
Sim.v = np.array([0., 60.0, 0.]) # 雷达速度 m/s
Sim.vt = np.array([20., 30., 5.]) # 目标速度 v-target
Sim.dt = 0.00004 # 40us
A, B = Sim.run_no_rotation()
print("gt:", Sim.vt)
print("estimation:", (np.linalg.pinv(A)@B + Sim.v).round(3))
gt: [20. 30. 5.]
estimation: [20.215 29.951 5.138]
Sim.w = np.array([0., 0., np.deg2rad(10)]) # 角速度
Sim.v = np.array([0., 60.0, 0.]) # 雷达速度 m/s
Sim.vt = np.array([20., 30., 5.]) # 目标速度 v-target
Sim.dt = 0.00004 # 40us
A, B = Sim.run_no_rotation()
print("gt:", Sim.vt)
print("estimation:", (np.linalg.pinv(A)@B + Sim.v).round(3))
gt: [20. 30. 5.]
estimation: [20.072 29.984 5.046]
Sim.w = np.array([0., 0., np.deg2rad(30)]) # 角速度
Sim.v = np.array([0., 10.0, 0.]) # 雷达速度 m/s
Sim.vt = np.array([20., 30., 5.]) # 目标速度 v-target
Sim.dt = 0.001 # 1ms
A, B = Sim.run_no_rotation()
print("gt:", Sim.vt)
print("estimation:", (np.linalg.pinv(A)@B + Sim.v).round(3))
gt: [20. 30. 5.]
estimation: [23.385 29.235 7.141]
Sim.w = np.array([0., 0., np.deg2rad(30)]) # 角速度
Sim.v = np.array([0., 60.0, 0.]) # 雷达速度 m/s
Sim.vt = np.array([0., 0., 1.]) # 目标速度 v-target
Sim.dt = 0.001 # 1ms
A, B = Sim.run_no_rotation()
print("gt:", Sim.vt)
print("estimation:", (np.linalg.pinv(A)@B + Sim.v).round(3))
gt: [0. 0. 1.]
estimation: [ 2.711 -0.615 2.788]
Sim.w = np.array([0., 0., np.deg2rad(5)]) # 角速度
Sim.v = np.array([0., 60.0, 0.]) # 雷达速度 m/s
Sim.vt = np.array([0., 0., 1.]) # 目标速度 v-target
Sim.dt = 0.001 # 1ms
A, B = Sim.run_no_rotation()
print("gt:", Sim.vt)
print("estimation:", (np.linalg.pinv(A)@B + Sim.v).round(3))
gt: [0. 0. 1.]
estimation: [ 0.454 -0.103 1.299]
Sim.w = np.array([0., 0., np.deg2rad(5)]) # 角速度
Sim.v = np.array([0., 60.0, 0.]) # 雷达速度 m/s
Sim.vt = np.array([20., 70., 1.]) # 目标速度 v-target
Sim.dt = 0.005 # 5ms
A, B = Sim.run_no_rotation()
print("gt:", Sim.vt)
print("estimation:", (np.linalg.pinv(A)@B + Sim.v).round(3))
gt: [20. 70. 1.]
estimation: [26.439 68.541 5.152]
由于Aqronos雷达目标是逐行扫描（100ms/帧），如果总共20行，那么意味着上下两条线上点的间隔能差5ms。从上述仿真结果可以看出，即使雷达转动速度很低（5°/s），对目标速度方向求解有较大影响。